本文主要介绍了线性结构的典型代表——线性表的逻辑结构和抽象数据结构.
目录（更新中）
参考资料
[1] 王红梅编著. 数据结构（C++版本）（第2版）.
北京：清华大学出版社，2011.
[2] 张铭. coursera-数据结构基础.
coursera.
线性结构
根据前文的讨论，数据结构主要有集合、线性结构、树结构、图结构四大类，本文要讨论的线性表正是线性结构的典型代表.
除线性表外，线性结构用可根据不同标准分为许多类型：
按复杂程度划分
- 简单的：线性表、栈、队列、散列表
- 高级的：广义表、多维数组、文件……
按访问方式划分
- 直接访问型（direct access)
- 顺序访问型（sequential access）
- 目录索引型（directory access）
按操作划分
本文讨论的线性表是线性结构的典型代表.
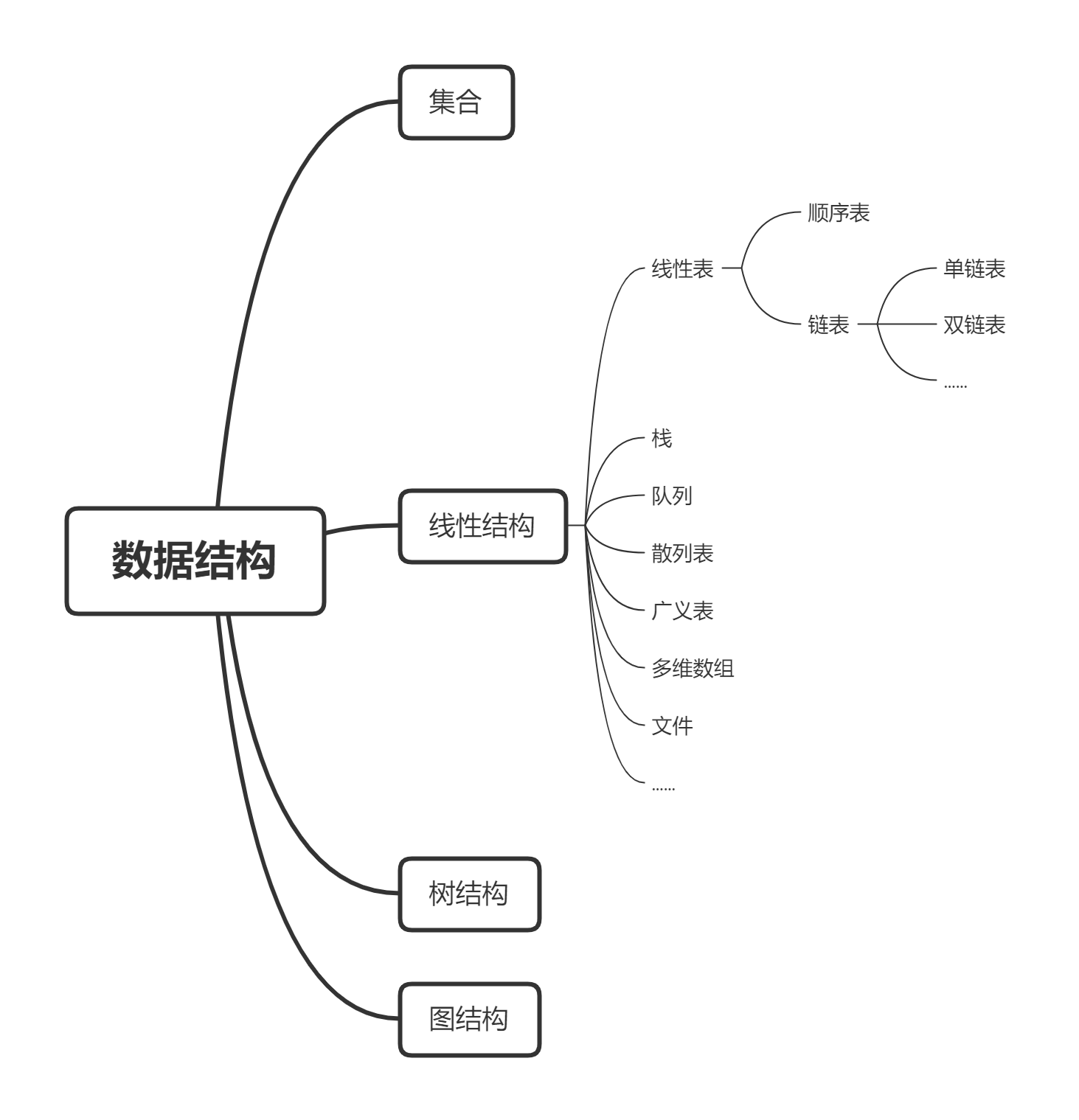图 3-1 数据结构的分类
线性表的定义
线性表（linear list）简称表，是
个具有相同类型的数据元素的有限序列，线性表中数据元素的个数称为线性表的长度.
长度等于零时称为空表，一个非空表通常记为：
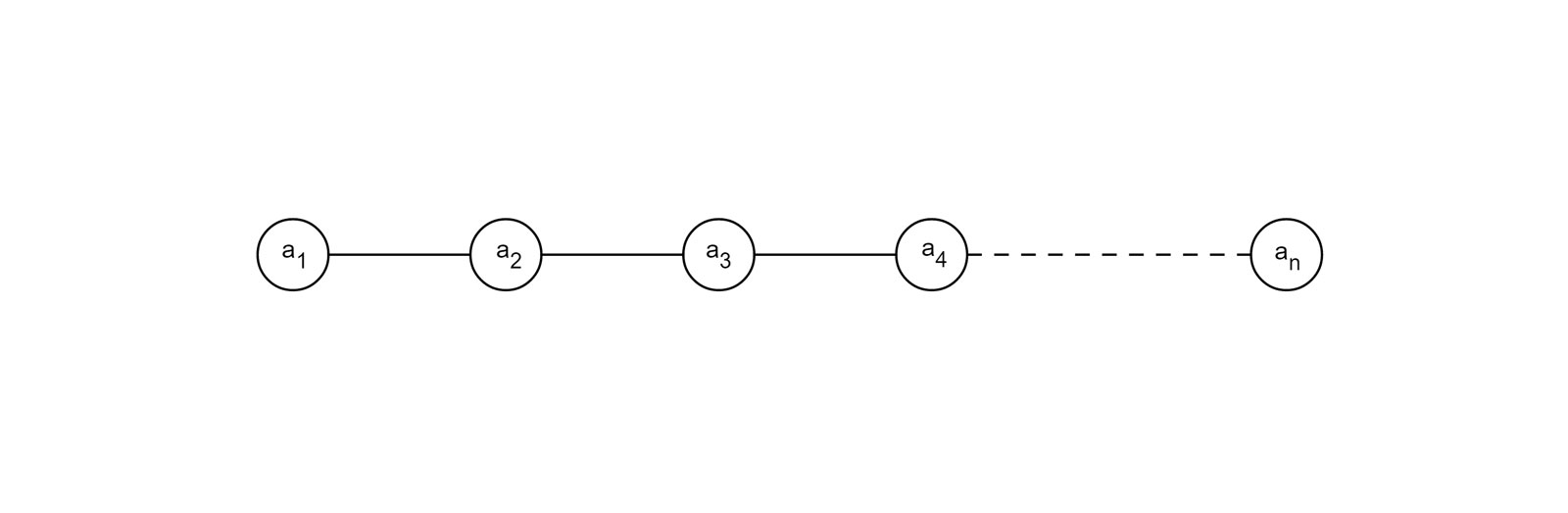图 3-2 线性表示意图
其中， 称为数据元素，小脚标
表示该元素在线性表中的位置或序号. 任意一堆相邻的数据元素 和
之间存在序偶关系 ，且 称为 的前驱， 称为 的后继.
线性表的数据元素具有抽象（即不确定）的数据类型，在具体的应用程序中被具体的数据类型所替代.
具体地，线性表具备以下特点：
均匀性：虽然不同线性表的数据元素可以是各种各样的，但对于同一线性表的各数据元素必定具有相同的数据类型和长度.
有序性：各数据元素在线性表中都有自己的位置，且数据元素之间的相对位置是线性的.
线性表的抽象数据类型定义
线性表应当满足存取访问、插入和删除等操作.
可将其抽象数据类型定义如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
|
ADT List
Data
线性表中的数据元素具有相同的类型，相邻元素具有前驱和后继关系.
Operation
InitList
前置条件：线性表不存在
输入：无
功能：线性表的初始化
输出：无
后置条件：一个空的线性表
DestoryList
前置条件：线性表已存在
输入：无
功能：销毁线性表
输出：无
后置条件：释放线性表所占用的存储空间
Length
前置条件：线性表已存在
输入：无
功能：求线性表的长度
输出：线性表中数据元素的个数
后置条件：线性表不变
Get
前置条件：线性表已存在
输入：元素的序号 i
功能：按位查找，在线性表中查找序号为 i 的数据元素
输出：若序号合法，返回序号为 i 的元素值，否则抛出异常
后置条件：线性表不变
Locate
前置条件：线性表已存在
输入：数据元素 x
功能：按值查找，在线性表中查找值等于 x 的元素
输出：若查找成功，返回元素 x 在表中的序号，否则返回 0
后置条件：线性表不变
Insert
前置条件：线性表已存在
输入：插入位置 i；待插元素 x
功能：插入操作，在线性表的第 i 个位置插入一个新元素 x
输出：若插入不成功，抛出异常
后置条件：若插入成功，表中增加了一个新元素
Delete
前置条件：线性表已存在
输入：删除位置 i
功能：删除操作，删除线性表中的第 i 个元素
输出：若删除成功，则返回被删元素，否则抛出异常
后置条件：若删除成功，表中减少被删元素
IsEmpty
前置条件：线性表已存在
输入：无
功能：判空操作，判断线性表是否为空
输出：若是空表，返回 1，否则返回 0
后置条件：线性表不变
PritList
前置条件：线性表已存在
输入：无
功能：遍历操作，按序号依次输出线性表中的元素
输出：线性表中的各个数据元素
后置条件：线性表不变
endADT
|
需要注意的是：
对于不同的应用，线性表包含的基本操作可能不同，同名操作的实现细节可能不能.
对于实际问题中更复杂的操作，可以用这些基本操作的组合来实现.
如按值删除，可以通过上述定义的 Locate 和
Deleta 操作的组合实现.
